2018-2019 Academic Year Colloquium Schedule |
|
September 13, 2018
| Title: |
Casino Carnival Games: Past, Present, and Future
|
| Speaker: | Mark Bollman
Professor of Mathematics
Mathematics and Computer Science
Albion College
Albion, MI
|
| Abstract: |
Beyond the "big four" casino table games of baccarat, blackjack, craps, and roulette, over 1000 different games have been designed, proposed for casino use, and approved by the state of Nevada. In this presentation, we shall look at the math behind some of the games that have fallen by the wayside and at the mathematical issues that arise in designing a new game of chance. An opportunity to investigate the mathematics behind a new game proposal will be announced.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
September 20, 2018
September 27, 2018
| Title: |
Reducibility and Balanced Intransitive Dice
|
| Speaker: | Michael Ivanitskiy1 and Michael A. Jones2
1University of Michigan; 2Mathematical Reviews
Ann Arbor, MI
|
| Abstract: |
We will review some results about balanced intransitive $n$-sided dice and what it means for a set of dice to be reducible based on a concatenation operation. Using data from the Online Encyclopedia of Integer Sequences, the lexicographical ordering of dice, and permutations, we are able to construct new integer sequences representing the number of $n$-sided reducible and irreducible dice. We define a notion of margin and explain how margins are effected by concatenation. We introduce a new splicing operation that generalizes concatenation and give conditions for when the resulting dice are balanced and irreducible. Finally, we construct new integer sequences for the number of fair, balanced dice and the largest margins for $n$-sided, balanced intransitive dice.
Bonus: You will either get to make or will be given a set of balanced, intransitive dice.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
October 4, 2018
| Title: |
Multi-Lens Analysis of Office Dynamics and
Space Usage
|
| Speaker: | Angela Morrison, '17
Graduate Student
Mathematics
Michigan State University
East Lansing, Michigan
|
| Abstract: |
Workplace optimization is critical for organizations to make the most of their real estate as well as help employees stay more productive at work. Steelcase Space Analytics equips organizations with tools and data needed to measure and improve the effectiveness of the workplace by applying their proprietary sensing capability. This project aims to analyze office space dynamics and usage by investigating correlations between and within sensing and survey datasets sourced from Steelcase's 2 West (2W) facility. The data consists of sensor output that describes how often spaces are in use, as well as survey data that reports how the 2W employees feel about using certain spaces. Clustering analysis was developed to study the hidden trends of the sensor data and generalized linear mixed model (GLLM) was constructed to investigate the correlations between the sensor data and space traits data. The results showed that the significant space traits indicated by the GLMM were also the popular ones from survey data analysis.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
October 11, 2018
| Title: |
Spherical Panoramic Photographic Processing
|
| Speaker: | David A. Reimann
Professor
Mathematics and
Computer Science
Albion College
Albion, Michigan
|
| Abstract: |
Conventional cameras view a small solid angle, limiting the both the field of view and projective distortion. However, multiple individual pictures are need to have full spherical coverage.
Cameras that can directly take spherical panoramic photos, such as the Ricoh Theta S, have become available as relatively inexpensive consumer products.
Unlike a traditional camera, this camera has two hemispherical lenses, allowing it to see simultaneously in every direction around the camera.
These cameras produce an equirectangular projection, where each latitude row has the same number of pixels, which has severe distortion at the poles.
One approach to hardcopy display is to map the image onto the surface of a small polyhedron, such as a Platonic or Archimedean solid, which reduces the distortion.
Using such polyhedra resembles the process artist Dick Termes uses for painting on a sphere, which he calls a Termesphere. These techniques force the viewer to
see the world inside-out.
This work maps the spherical photo to the inside of a large polyhedra to create a miniature pavilion which can be entered for a personal panoramic experience.
Other interesting applications and issues will be discussed.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
October 25, 2018
| Title: |
Solving an Easy Equation in an Interesting Way
|
| Speaker: | Mckenzie West
Visiting Assistant Professor
Mathematics
Kalamazoo College
Kalamazoo, Michigan
|
| Abstract: |
In number theory, we are interested in studying the behavior of integers. For example, Fermat's Last Theorem classifies all triplets of integers that satisfy $x^n+y^n=z^n$. In this talk, we will look at a special collection of "integers", the $S$-units, and determine every solution to the equation $x+y=1$. We will draw from areas such as linear algebra, geometry, and computer algorithms in this talk as we cover my relation to the $S$-unit equation and its applications.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
November 8, 2018
| Title: |
Mathematics and Computer Science in Sports
|
| Speaker: | Jon Lorenz
Business Analyst
Business Strategy and Analytics
Detroit Lions
Detroit, MI
|
| Abstract: |
The sports industry is incredibly competitive. How do we find business advantages through computer science and mathematics? I will walk through my own personal path to working in the NFL, what kind of analysis and contributions I make on a daily basis, how math and CS are essential to best business practices, and what opportunities are arising with the Lions this winter.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
November 15, 2018
| Title: |
The Geometry of Polynomials
|
| Speaker: | Matt Boelkins
Professor of Mathematics, Grand Valley State University
Mathematics
Grand Valley State University
Allendale, MI
|
| Abstract: |
In the geometry of polynomials, we seek to understand relationships among certain sets connected to polynomial functions. For example, Marden's Theorem reveals stunning connections between the critical numbers of a cubic polynomial with complex zeros and the inscribed in-ellipse of the triangle whose vertices are the polynomial's zeros.
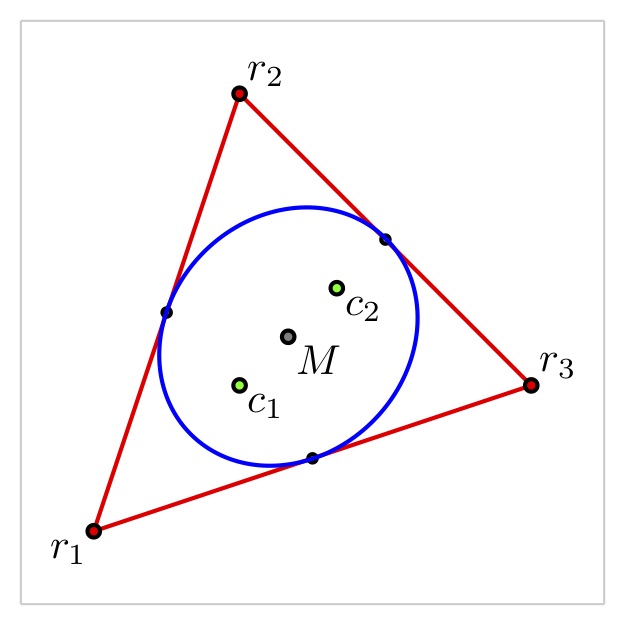
In this talk, we'll discuss several important historical results from the geometry of polynomials and survey developments in the past 25 years that are centered on polynomial root-dragging, the study of how continuously changing one or more roots of a polynomial function affects various properties of the function. We will encounter some surprising structural results about polynomial functions that deserve to be more well-known and also see beautiful interplay between calculus and Euclidean geometry.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
November 29, 2018
| Title: |
Random Walks and Ito Calculus with Applications to Finance
|
| Speaker: | Darren E. Mason
Professor
Mathematics & Computer Science
Albion College
Albion, MI
|
| Abstract: |
Rational pricing of many financial products rely on mathematical modeling of random phenomena (e.g. the time evolution of a stock price). In this talk I will discuss the fundamental ideas of random walks, Brownian motion, and Ito Calculus, with applications actuarial science and finance. This presentation also serves as a nice introduction to what can be expected by students in the last portion of the topics course Math 389 being offered in Spring 2019.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
February 7, 2019
| Title: |
How path counting and electrical resistance can help us find hidden links in social networks.
|
| Speaker: | Amanda Francis
Associate Editor
Mathematical Reviews
American Mathematics Society
Ann Arbor, Michigan
|
| Abstract: |
Given a network of known relationships between people in a social network, can we predict new or hidden relationships? There are several known methods for link prediction. For example, the Katz method counts the number of paths between people, and assigns likelihood scores based on these counts. Alternately, we can use the mathematics of electrical resistor networks, assigning scores based on resistance distance between pairs of nodes. In this talk I will describe some of the mathematics behind these link prediction algorithms. I will share some new results about computing effective resistance on certain families of graphs, and I will discuss open problems, including comparing link scoring methods on simple networks.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
February 14, 2019
| Title: |
Fibonacci's New Math
|
| Speaker: | Ellen Kamischke
Instructor
Mathematical Sciences
Michigan Technological University
Houghton, MI
|
| Abstract: |
The publication of Liber Abaci, Leonardo Pisano's book of calculation, in 1202 introduced the use of the Hindu-Arabic numeration system across Europe. The techniques of arithmetic and problem solving explained here were drawn from Leonardo's education and travels throughout the world of the late 12th century. Leonardo, who was also known as Fibonacci, wrote several books on mathematics following the Liber Abaci. While not widely appreciated, this work along with Fibonacci's other writings, played an important first role in reviving mathematics in Europe. In this talk we will examine some of the techniques introduced in the Liber Abaci and explore some of the problems presented there using both his methods and those of contemporary algebra. We will also look at some of the techniques presented in this book from 1202 that are still in use today.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
February 21, 2019
| Title: |
Combinatorial, Geometrical, and Analytical Aspects of Random Walks in Domains with Boundary
|
| Speaker: | Dorin Dumitrascu
Associate Professor of Mathematics
Mathematics
Adrian College
Adrian, MI
|
| Abstract: |
The talk will present some interesting combinatorial and geometrical symmetries of the distribution of random walks on domains with boundary.
Naively, a random walk of length n consists of n consecutive "moves" (up, down, left, or right) on the lattice of integer points in the plane. Let Δ be an infinite domain in the Euclidean plane with boundary ∂Δ. I will give explicit formulas for the probability of a random walk to exit Δ at a precise point on ∂Δ.
The justification of such formulas presents meaningful connections with linear algebra, probability, geometry, and real analysis.
The talk is geared toward an undergraduate audience and exemplifies a possible "capstone" topic for our curriculum.
This is joint work with Jamie Brandon, currently at Brandeis University.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
February 28, 2019
March 21, 2019
| Title: |
Internal Symmetries in Musical 12-Tone Rows
|
| Speaker: | Anil Venkatesh
Assistant Professor of Mathematics
Mathematics
Ferris State University
Big Rapids, MI
|
| Abstract: |
In music, a 12-tone row is any of the 12! possible orderings of notes in
the Western chromatic scale. The musical notes of a 12-tone composition
must always arise in the same order, cycling repeatedly through a
predetermined "row" of twelve notes. The repetitive structure of
12-tone music lends itself to mathematical study. In 2003, Hunter and
von Hippel investigated symmetry in 12-tone rows, using group theory to
enumerate equivalence classes of rows under a group of music-theoretic
symmetries. They found that highly symmetric rows constitute just 0.13%
of the 12! possibilities, and yet these rows arise in 10% of actual
compositions. This result provided strong evidence that composers favor
symmetric rows, but leaves us wondering about the remaining 90% of
compositions. In this talk, we introduce a way to measure the occurrence
of short repetitions and symmetries that go undetected in the analysis of
Hunter and von Hippel. We present a new hierarchy of symmetry for 12-tone
rows, and offer evidence that composers favor symmetric substructures
in their work.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
March 28, 2019
| Title: |
Mathematical Inverse Problems
|
| Speaker: | Zoe Dai
Professor of Mathematics
Mathematics and Computer Science
Alma College
Alma, Michigan
|
| Abstract: |
Inverse problems arise frequently in many areas of scientific research, and have very wide application, such as in seismology, medical imaging, remote sensing, and image reconstruction.
I will introduce the topic and describe the challenges involved in solving inverse problems. Several techniques for meeting these challenges will then be presented, and their advantages and disadvantages described.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
April 4, 2019
| Title: |
Newton-like Identities from Synthetic Division
|
| Speaker: | Michael A. Jones
Associate Editor
Mathematical Reviews
American Mathematical Society
Ann Arbor, MI
|
| Abstract: |
I will recall and then prove Vieta's formulas that relate the roots of a polynomial to its coefficients. I will explain Euler's proof of Newton's identities that relate the coefficients of a polynomial to the sums of powers of its roots. Finally, I'll explain how to view synthetic division from a linear algebra point of view and use this approach to prove an identity in the spirit of Newton.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
April 11, 2019
| Title: |
Utilizing Deep Learning and Machine Learning Algorithms in Disease Prediction
|
| Speaker: | Buket Aydas
Assistant Professor of Computer Science
Department of Mathematics and Computer Science
Albion College
Albion, MI
|
| Abstract: |
Metabolomics, proteomics, and genomics (in general omics) hold
the promise as a new technology to diagnose highly heterogeneous
diseases. Conventionally, omics data analysis for diagnosis is done
using various statistical and machine learning based classification
methods. However, it remains unknown if deep neural network, a class of
increasingly popular machine learning methods, is suitable to classify
omics data. Here we use omics data to test the accuracies of feedforward
networks, a deep learning (DL) framework, as well as five widely used
machine learning models, namely random forest (RF), support vector
machines (SVM), linear discriminant analysis (LDA), prediction analysis
for microarrays (PAM), and generalized linear models (GLM) to predict
some very important diseases. DL framework resulted in higher predictive
power in classifying cases/controls, compared to the other five machine
learning algorithms. Some of the diseases that we work to predict are
pancreatic cancer, cervical cancer, autism, down syndrome, cerebral palsy, pediatric
concussion, miscarriage and Alzheimer disease.
|
| Location: |
Palenske 227
|
| Time: |
3:30 PM
|
| Citation | Click for BibTeX citation |
| Flyer | Click for a printable flyer |
|

