Using Original Research in an AP or Advanced Statistics Course
Lindsay Noakes and Mary Schroth
Battle Creek Area Mathematics and Science Center
Battle Creek, MI
lindsay.noakes@bcmsc.k12.mi.us
Mark Bollman→
Albion College
Albion, MI
National Council of Teachers of Mathematics
2005 Annual Meeting and Exposition
Anaheim, CA
9 April 2005
Contents
Research in an AP Statistics Course: Why Take the Time?
Project #1 – Experimental Design and Descriptive Data
Project #1 – Experimental Design and Descriptive Data Rubric
The Best "Milk and Cookie" Cookie?
Project #2: T-Curves and T-Tests
Tape Brand Comparison for Stickiness
Critical Research Concerns and Report Style Guide for Research Papers
Project #3 – Observational Study and Analysis
Knowledge of Current Events vs. Political Affiliation
This work was supported in part by a grant from the Hewlett-Mellon Fund for Faculty Development at Albion College, Albion, Michigan.
Research in an AP Statistics Course: Why Take the Time?
Selection from the AP Statistics Topic Outline:
II. Sampling and Experimentation: Planning and conducting a study (10%-15%)
Data must be collected according to a well-developed plan if valid information on a conjecture is to be obtained. This plan includes clarifying the question and deciding upon a method of data collection and analysis.
A. Overview of methods of data collection
1. Census
2. Sample survey
3. Experiment
4. Observational study
B. Planning and conducting surveys
1. Characteristics of a well-designed and well-conducted survey
2. Populations, samples, and random selection
3. Sources of bias in sampling and surveys
4. Sampling methods, including simple random sampling, stratified random sampling, and cluster sampling
C. Planning and conducting experiments
1. Characteristics of a well-designed and well-conducted experiment
2. Treatments, control groups, experimental units, random assignments, and replication
3. Sources of bias and confounding, including placebo effect and blinding
4. Completely randomized design
5. Randomized block design, including matched pairs design
D. Generalizability of results and types of conclusions that can be drawn from observational studies, experiments, and surveys.
Conducting hands-on research is a much more interesting and effective way for students to learn the objectives stated above. Although conducting research takes considerably more time than lecturing, the benefits far outweigh the costs.
Project #1 – Experimental Design and Descriptive Data
A.P. Statistics & Adv. Statistics
Battle Creek Area Math & Science Center
Project Objective
The end goal of this project is a 5-7 page paper in which you report the results of a study that you design and implement. The study must be designed and reported within the parameters given below. The main point of this project is to give you experience dealing with the issues concerning designing and implementing a valid scientific study.
Keep this in mind as you do your write up: It is most important that you make clear your knowledge of the important issues of study design, and the strengths or weaknesses of your particular design. You should do the best design you can do, but you will not be graded down for not having a perfect study. However, you will be graded down if you fail to specify in your report how your study is imperfect and what the implications of the imperfections are for your results.
Research Teams
You must work on a team of either 3 or 4 people. You must all work on the experiment together from beginning to end. Each member of your team will all use the same data for your report.
You MUST DO YOUR OWN REPORT, including creating all graphics and doing all of the numeric work yourself. If there is any indication that any part of any report was shared with some other person, all individuals involved will receive a grade of ZERO and parents will be notified.
Research Topic
You are to select a topic:
a) that can be studied with a simple scientific experiment
b) whose results can be reported as measurements (e.g., times, weights, lengths, etc.)
c) that has been O.K.’ed by the instructor
Study Design
The study must be designed in such a way that its implementation:
a) utilizes randomization at every possible step
b) has at least two treatments
c) maintains as much control as possible given realistic limitations
d) involves at least 30 experimental units.
Results
For this project, you will only need to report and describe your data. We will not be doing any statistical inference for this project, so we will not be drawing any specific statistical conclusions as to what the data say about the population. However, you should make some general conclusions as to what your results suggest about the affects of the treatments. Later on in the year we will revisit this project and do some statistical inference.
Grading
This report will be worth 100 points. It will be graded on two sets of criteria. 20 points will be based on the format and neatness of the report, 20 points on the experimental design, and 60 points on the thoroughness of your descriptions of the design, implementation, and conclusions. The report must be formatted and contain all information as described on the next page.
Report Requirements
Format and Style
All of the text in your report must be typed. All graphics must be computer generated. The report must contain the following:
a) Title page indicating name of study, your name, course name, and instructor’s name. Use at largest size 14 font (larger is unprofessional).
b) Separate sections titled as noted below which meet all of the requirements listed below. Double space the lines throughout.
c) One appendix that shows all of your raw data.
Section 1: Introduction
Begin with a statement of the topic of study. Be sure to note why this topic is interesting to you and or anyone else. Then give a brief statement of what you were looking to find in the study and make a hypothesis about what you expected to find.
Section 2: Study Design
Here you must accomplish several things:
a) Describe the population of interest and what you will be studying
b) Describe the experimental design. Be sure to include a full description of the blocking and treatments, and include a flowchart of the design (see the book for examples).
c) Describe how randomization was used.
d) Describe how control was maintained
Section 3: Design and Implementation Concerns
Describe any concerns you have about the methods by which you carried out your experiment. If there were any possible sources of bias, or any problems with getting a truly random sample, these must be noted here.
Section 4: Findings
Give the results of your study. That is, show your data in some graphical form and describe and compare the distributions between blocks and treatments. This might require as many as 4–6 graphs to capture distributions by block and factor. Be sure to comment on each graph and refer to specific numeric descriptors of spread and center. Be sure to refer to the actual data in the Appendix.
Section 5: Conclusions
Although you will not be doing any “official” statistical inference, draw whatever conclusion you believe you can safely draw about the population in question. Note whether or not your hypothesis appears to have been correct. If you had serious design flaws noted in section 3, be sure to explain how those flaws affect your conclusions.
Section 6: Appendix
A table including all data collected.
Fill out the information below. Be specific so that I can give you specific feedback.
Topic of the Study: _______________________________________________________________
Question you hope to answer with the study:
______________________________________________________________________________
______________________________________________________________________________
What exactly will you be measuring and how will you measure it?
______________________________________________________________________________
______________________________________________________________________________
What will your blocks be?
______________________________________________________________________________
What will your treatments be?
_____________________________________________________________________________
______________________________________________________________________________
What do you expect to find? (i.e., What is your hypothesis?) ______________________________________________________________________________
______________________________________________________________________________
______________________________________________________________________________
Group Members:
____________________________
____________________________
____________________________
____________________________
____________________________________
Teacher Signature
This proposal is due on or before _____________. Each day it is late will result in a 5% reduction of the overall project grade. You are not to begin implementing this project until you have the instructor’s signature on this piece of paper.
Project #1 – Experimental Design and Descriptive Data RubricAdv. Statistics/A.P. Statistics – 2004/2005 – Schroth/Noakes
Format and Neatness /20
All of the text in your report must be typed _____
Graphics computer generated _____
Title page, size 14 font max _____
Quality of Experimental Design /20
Utilizes randomization at every possible step _____
Maintains as much control as possible _____
30 experimental units _____
Two treatments _____
Quality of Written Report /60
Section 1: Introduction _____
Statement of the topic _____
Why topic is interesting _____
Statement of what you were looking to find _____
Hypothesis _____
Section 2: Study Design
Describe population _____
Describe experimental design _____
blocking (if any) _____
treatments _____
flow chart (includes statement of randomization) _____
Describe how randomization was used. _____
Describe how control was maintained _____
Section 3: Design and Implementation Concerns
Possible sources of bias _____
Problems getting truly random sample _____
Implications of the imperfections for your results. _____
Section 4: Findings
Data in graphical form _____
Describe and compare results by block _____
Describe and compare results by treatment _____
Comment on each graph _____
Specific numeric descriptors of spread and center _____
Reference to actual data in appendix _____
Section 5: Conclusions
Conclusion about population _____
Reference to hypothesis _____
How design flaws affect your conclusions _____
Section 6: Appendix
Table of all data _____
The Best "Milk and Cookie" Cookie?
Advanced Statistics
Mrs. Noakes
Introduction
It is a fact that people like cookies. It doesn't take statistics to figure that out. Cookie sales are never low in the United States. One thing that may need to be addressed is how people like their cookies when they eat them. Do they like them firm and crumbly, or moist and chewy? This is what our experimental lab is all about.
We will take a sample of cookies from the population or container of cookies and will test the absorbency of these cookies in two different liquids. These two liquids are 2% milk and Hawaiian Punch. We will see which cookies absorb the most liquid and how the two different liquids are absorbed by the cookies.
We will be measuring the mass difference and comparing these values in terms of type of cookie and in terms of type of treatment or liquid. A larger % mass difference value tells us that the cookie absorbed more of the liquid. Other pieces of data that will be looked at are the mean value of % mass differences and the standard deviation of the % mass differences.
The results of this experiment can be interesting to several groups of people and for different reasons. The results could be interesting to little kids who want to know what type of cookie to dunk in the 2% milk they have a surplus of (so they don't have to race the evil expiration date). The results could also be very useful to a cookie company that will want to formulate ways to make their cookie production more consistent (the s.d. of the % mass differences will tell us how consistent the cookies are created).
The consensus opinion of our group is that a cookie with a high liquid absorbency is not a good cookie. Therefore we are saying that the cookie that retains the least amount of liquid will be the best "milk and cookie" cookie. We are hypothesizing.that the Oreos will retain the least liquid and therefore be the best cookie while the Pecan Classics will retain the most liquid and therefore will be the worst cookie.
Study Design
As stated in the introduction, the population was a single package of cookies and the sample was 6 cookies taken systematically from that package. Three of these six cookies were used for each treatment. The two treatments were 2% milk and Hawaiian Punch. Both treatments were bought in 2-liter containers.
Now the procedure of the lab will be discussed. We procured the following items for the lab procedure.
5 packages of cookies
1 Package Nabisco Brand Chips Ahoy Cookies
1 Package Meijer Brand Vanilla Wafers
1 Package Nabisco Brand Oreos
1 Package Meijer Brand Pecan Classics
1 Package Nabisco Brand Nutter Butters
2 500 ml Glass Flasks
1 Wire Mesh Net
1 Analytical Scale
A large amount of paper towels
1 Stopwatch (Calculator Application was used for this experiment)
Cookies are selected systematically from the population pack of cookies. This is done by selecting each sixth cookie and using that one for the experiment. We kept three extra cookies of each type in case we needed them.
We took each cookie and weighed it on the scale. This was recorded as the initial weight of the cookie in the data tables.
We wrapped the cookie in the wire mesh and totally immersed the cookie in the given treatment. We left it in the liquid for twenty seconds and then lifted it out and allowed it to drip off excess liquid for ten seconds before we put it back on the scale to find the ending weight for the cookie.
Below is a representation of the procedure in schematic form.
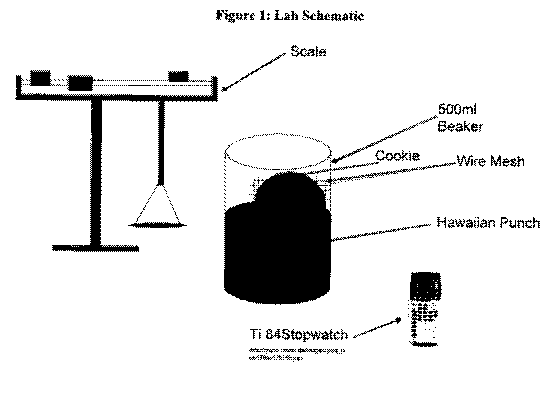
Now the lab calculations will be listed. To find the mass difference of a given cookie, the formula is Ending Mass - Initial Mass = Mass Difference. This value is then divided by the initial mass to find the % weight difference. The formula is Mass Difference/Initial Mass = % Weight Difference.
The mean of the % weight difference is calculated by adding up the weight differences for a given cookie and dividing that number by three. The standard deviation for a given cookie is also calculated by finding the s.d. using the mean of the weight differences. This was done on our calculator and therefore the formula was stored and resolved on the calculator.
These calculations will be used to analyze things in the conclusions section. To control the experiment, we used a block design. Below is a representation of this block design.
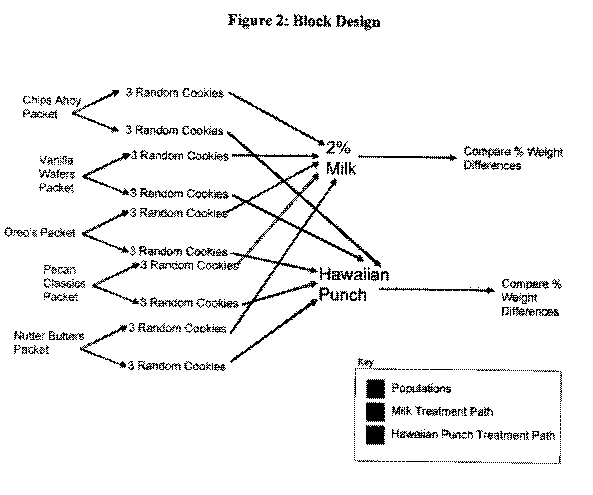
The above diagram is called the block control method because it is this method that is used to control the experiment. It makes sure that all of the variables in the experiment are accounted for. This also makes it possible to keep the experiment random. Due to the fact that we used a systematically random sample of cookies from the population, we are keeping the variable random.
Design and Implementation Concerns
Several problems could have occurred with this experiment and there may have been several flaws in the design of the lab. It is important to acknowledge these so sources of error in results may be clearer.
In the realm of our lab procedure, we used two treatments, 2% milk and Hawaiian Punch. It would have been better if we had used a third as a control such as water. We could have compared both of the treatments to the control water. We used a smaller sample than I would have hoped to use (3 cookies of each type for each treatment) but the fact that we purchased the cookies influenced how many we used. We had to use counterbalance scales instead of more exact digital scales and this made it hard to mass the cookies. Though this was a very minor issue, it may have affected our results. The type of scales also limited the time we had to do the lab and this is one of the reasons we didn't use water as a control treatment. Having the population be so small was a problem in that we couldn't be sure that a given package of cookies was a good representation of the actual population of all like cookies. We accepted the fact that this could be a problem and went on with the experiment.
There was not much bias in the lab and we strove to keep the person that did each job constant to cut down on discrepancies.
Findings
By looking at the graphs (next page), we can see that the most absorbent cookie is Pecan Classic while the least absorbent cookie is the Nutter Butter. We can also see that Vanilla Wafers have a S.D. that far exceeds that of any other of the cookie types. We will visit this idea in the conclusion section. The data in this section can be found in the appendix.
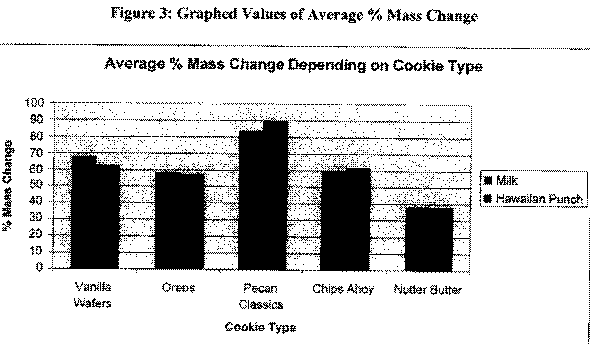
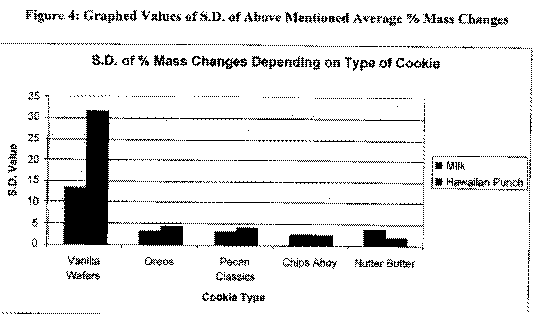
Conclusions
The two graphs shown above in the findings section will be used several times in the conclusions section to draw necessary conclusions about our data. In our hypothesis, we said that Oreos would be the least absorbent cookies while Pecan Classics would be the most absorbent. Looking at figure three, we see that our hypothesis was only half correct. Indeed, the Pecan Classics were the most absorbent as their average % mass change was 20% more than the second most absorbent, Vanilla Wafers. We were incorrect in hypothesizing that Oreos would be the least absorbent. In fact; the Nutter Butters were the least absorbent. The Nutter Butters were about 20% less absorbent than the Oreos so we were incorrect in our hypothesis. Therefore in conclusion for this part, I accept my hypothesis that Pecan Classics were the most absorbent cookie and I reject my hypothesis that Oreos are the least absorbent and correct it by saying that Nutter Butters are the least. Therefore according to our group, Pecan Classics are the worst "Milk and Cookie" Cookie and Nutter Butters are the best.
We can now look at the graph of S.D. values. This will tell us how consistently the cookies are made. The least consistently made cookie is the Vanilla Wafer. It has a very high s.d. of % mass differences. That means that Vanilla Wafers are cheaply made. The other cookies are about even in consistency and therefore are not cheaply made.
By looking at figure three, based on the majority of our findings, I can say that Hawaiian Punch is the liquid that is absorbed more. These things can be concluded by looking at these graphs and the data tables in the appendix.
Appendix 1: Vanilla Wafers in Milk
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
3.795 |
3.392 |
3.645 |
3.610667 |
Final Mass |
6.25 |
5.355 |
6.7 |
6.101667 |
% Mass Change |
64.69038 |
57.87146 |
83.81344 |
68.79176 |
Mean % Weight Change |
68.79176 |
|||
SD of % Weight Change |
13.44852 |
|||
Appendix 2: Oreos in Milk
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
11.752 |
11.485 |
11.5 |
11.579 |
Final Mass |
18.595 |
17.82 |
18.582 |
18.33233 |
% Mass Change |
58.22839 |
55.15898 |
61.58261 |
58.3233 |
Mean % Weight Change |
58.3233 |
|||
SD of % Weight Change |
3.212904 |
|||
Appendix 3: Pecan Classics in Milk
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
15.285 |
15.3 |
15.765 |
15.45 |
Final Mass |
28.31 |
27.65 |
29.455 |
28.47167 |
% Mass Change |
85.21426 |
80.71895 |
86.83793 |
84.25705 |
Mean % Weight Change |
84.25705 |
|||
SD of % Weight Change |
3.169805 |
|||
Appendix 4: Chips Ahoy in Milk
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
10.825 |
11.29 |
11.58 |
11.23167 |
Final Mass |
17.735 |
18.05 |
18.35 |
18.045 |
% Mass Change |
63.83372 |
59.876 |
58.46287 |
60.72419 |
Mean % Weight Change |
60.72419 |
|||
SD of % Weight Change |
2.784078 |
|||
Appendix 5: Nutter Butters in Milk
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
13.905 |
14.72 |
14.625 |
14.41667 |
Final Mass |
19.89 |
20.395 |
19.745 |
20.01 |
% Mass Change |
43.04207 |
38.55299 |
35.00855 |
38.86787 |
Mean % Weight Change |
36.86787 |
|||
SD of % Weight Change |
4.026008 |
|||
Appendix 6: Vanilla Wafers in Hawaiian Punch
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
3.56 |
3.33 |
2.97 |
3.286667 |
Final Mass |
5.21 |
4.802 |
5.95 |
5.320667 |
% Mass Change |
46.34831 |
44.2042 |
100.3367 |
63.62974 |
Mean % Weight Change |
63.62974 |
|||
SD of % Weight Change |
31.80723 |
|||
Appendix 7: Oreos in Hawaiian Punch
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
11.65 |
12.13 |
12.14 |
11.97333 |
Final Mass |
18.98 |
18.72 |
18.865 |
18.855 |
% Mass Change |
62.91845 |
54.32811 |
55.39539 |
57.54732 |
Mean % Weight Change |
57.54732 |
|||
SD of % Weight Change |
4.682051 |
|||
Appendix 8: Pecan Classics in Hawaiian Punch
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
14.718 |
15.698 |
15.1 |
15.172 |
Final Mass |
28.891 |
29.647 |
29.62 |
29.386 |
% Mass Change |
96.29705 |
88.85845 |
96.15894 |
93.77148 |
Mean % Weight Change |
93.77148 |
|||
SD of % Weight Change |
4.255368 |
|||
Appendix 9: Chips Ahoy in Hawaiian Punch
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
11.14 |
10.9 |
11.9 |
11.31333 |
Final Mass |
18.15 |
18 |
19.05 |
18.4 |
% Mass Change |
62.92639 |
65.13761 |
60.08403 |
62.71601 |
Mean % Weight Change |
62.71601 |
|||
SD of % Weight Change |
2.53335 |
|||
Appendix 10: Nutter Butters in Hawaiian Punch
Cookie # |
1 |
2 |
3 |
Average |
Initial Mass |
14.6 |
14.485 |
14.387 |
14.49067 |
Final Mass |
20.185 |
19.86 |
20.3 |
20.115 |
% Mass Change |
38.25342 |
37.10735 |
41.0996 |
38.82013 |
Mean % Weight Change |
38.82013 |
|||
SD of % Weight Change |
2.055573 |
|||
What is your research question (remember that you must compare two measurements):
What are your experimental units?:
What exactly will you be measuring and how will you measure it?
What will your treatments be?
What do you expect to find? (i.e., What is your hypothesis?)
How will you control the experiment?
Group Members:
____________________________________
____________________________________
____________________________________
____________________________________
____________________________________
Teacher Signature
Each day that this proposal is late will result in a 5% reduction of the overall project grade. You are not to begin implementing this project until you have your instructor's signature on this piece of paper.
Project #2 - Rubric Name:________________________
Adv. Statistics/A.P. Statistics
Format and Neatness _____/20 |
All text typed (3) _____ Symbols computer generated and correct size (3) _____ Graphics computer generated and clear (5) _____ Figures and tables labeled and referred to in text (1) _____ 12 point Times (3) _____ 1.5 spaces per line (3) _____ Separate title page (2) _____ |
Quality of Experimental Design _____/30 |
Utilizes randomization at every possible step (10) _____ Maintains as much control as possible (10) _____ 30 experimental units minimum (5) _____ Two treatments (5) _____ |
Quality of Written Report _____/100 |
Section 1: Introduction Statement of the topic (3) _____ Why topic is interesting (3) _____ Statement of hypothesis (3) _____ Justification of hypothesis (2) _____ Section 2: Study Design Identify population clearly and correctly (3) _____ Describe experimental design flow chart (6) _____ Statement of randomization (2) _____ Note specific treatments (2) _____ Note exactly what quantity is being measured (2) _____ Section 3: Design and Implementation Concerns Correct identification of major concerns (5) _____ Explanation of bias issues related to each concern (5) _____ Problems getting truly random sample (3) _____ Section 4: Findings and Analysis Data in graphical form (3) _____ Describe and compare results by treatment (3) _____ Comment on each figure or table (3) _____ Specific numeric descriptors of spread and center (3) _____ Reference to actual data in appendix (1) _____ Test of significance Appropriate procedure (2-sample or matched pairs) (4) _____ Conditions checked(5) _____ Proper cautions noted if conditions not satisfied(3) _____ t statistics calculated appropriately (formula shown)(3) _____ P-value found with df reported(2) _____ Conclusion correct based on P-value(5) _____ 95% Confidence interval Calculation correct(3) _____ t* identified correctly(2) _____ Interpretation/conclusion correct(5) _____Section 5: Conclusions and Study LimitationsCorrect statement of conclusions regarding study(5) _____Reference to hypothesis(3) _____Full statement of how design flaws affect conclusions(3) _____Section 6: AppendicesA: Table of all data(3) _____B: Data collection tool (if appropriate)(3) _____ |
Project #2: T-Curves and T-Tests
January 3, 2005
Section 1: Introduction
The purpose of this project was to design an experiment where we would utilize the randomization process on a population and a t-test to conduct a study. We chose to study the effects of surrounding noise and the time it took for an individual to complete a memory game composed of simple playing cards. We chose this topic because it seemed like it would be fairly fun for the randomly selected individuals to participate in this type of experiment. Also, in choosing this experiment, I stated that for myself I tend to be able to think and act better in silence then with surrounding noise. However, a few of my lab partners stated that they work better when listening to music or watching the television. So, we also selected this experiment because we wanted to discover if more individuals perform better in silence or with music playing in the background. After discussing what we would be looking for in this experiment, we decided that individuals would be able to complete the memory game faster in silence then when there is music present in the background. This made sense to us because your mind is able to focus more on an assignment when there is nothing else present to distract it, such as music.
In conducting this experiment, we were looking to find which type of surrounding noise, silence or music provided by FM 104.9, would produce faster completion times of a memory game. Therefore, our hypothesis was that completion times of the memory game would be faster for an individual when they completed it in silence compared to when they completed the game with music in the background.
Section 2: Study Design
First, in designing this experiment, we had to choose our population. Our population was the combination of the individuals in the junior and senior classes at the Battle Creek Area Mathematics and Science Center (a.k.a. "The Center"). Next was the design of our experiment. Our general set-up was to have a memory game, composed of regular playing cards of all the same face color, set-up on a desk where an individual could sit and complete the game. We would then have a certain number of randomly selected individuals complete the memory game in silence first, then with music, and then have the other randomly selected individuals complete the memory game with music first, then in silence. During this time, we would record each individual's completion time of the memory game in silence and with the music so we would be able to perform a matched pairs test on the data. Also, after an individual had completed their test, whether in silence or with music first, we had them switch to a different memory game at another desk to eliminate more of the learning effect within our experiment. Once we had performed the necessary test with the data, we would then be able to make the proper conclusion on our hypothesis. Our Null Hypothesis, Ho, would be that the population difference would be equal to zero, μd = 0. Our Alternate Hypothesis, H1, would then be that the population difference would be greater than 0, μd > 0. In using the matched pairs test, the data for the completion times in silence would serve as the before data and the data for the completion times with music would serve as the after data. We would then proceed to find the differences by calculating the data after minus the data before.
The diagram below, Figure 1.1, illustrates our experimental design. The special treatments within our experiment were simply having the individuals complete the memory game in silence and with music from FM 104.9. The exact quantity that was being measured in this experiment was the time, in seconds, that it took for an individual to complete the memory game under the two treatments.
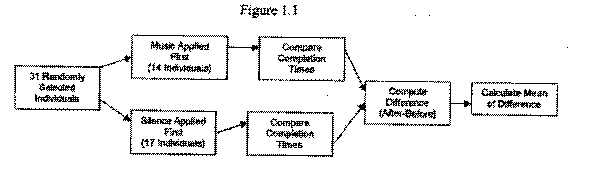
In designing this experiment, we needed to use randomization at every possible step. So, we first used our calculator and the random integer function to randomly select 37 students from the junior and senior classes. We did so by entering the command: randInt (97,212,37), into our calculator and recording 37 different random integers that appeared. If one set of output didn't contain all different numbers, we simply just kept entering the command until we had 37 different random integers. Once we had our numbers, we then took the student to which the number was assigned and contacted them for our experiment. Once we had 37 different random individuals, we needed to split them up in a way that a specific amount of them completed the memory game in silence first then with music, and then the other group would complete the memory game with music first and then in silence. This would decrease any learning effect in the experiment by an individual. We divided the 37 random individuals using a cluster type of randomization process. We took the 18 lowest integers selected in our simple random sample and placed the individuals assigned to that number in the group that would complete the memory game in silence first. We then took the 19 highest integers chosen in our S.R.S. and placed them in the group that would complete the memory game with music first.
We tested the two groups on a consecutive Tuesday and Wednesday. We assigned the group that would complete the memory game in silence first to Tuesday and the group that would complete the game with music first to Wednesday. There was no randomization used in assigning the specific groups to one of the two days however.
Section 3: Design and Implementation Concerns
In conducting this experiment there were some major concerns. There was the concern of being able to get at least 30 individuals to come and participate in our experiment and also the concern of where we would draw the lines on our population. Being able to get 30 individuals to play our game was a major concern because of the bias issues that surround it such as voluntary response and non-response, which almost go hand in hand. Voluntary response provided bias with this concern because from the 37 individuals we contacted to participate in our experiment; only 31 individuals were willing to participate. Those individuals who were interested in seeing what the experiment would be like came and played the memory game because they had an opinion or persuasion to do so. On the other hand, those individuals who didn't participate fit in with the bias issue of non-response. Those individuals who simply had no desire to be in our experiment or who were absent the days we were conducting the experiment, weren't present or weren't willing to participate. Also, those individuals who felt they wouldn't have time during our 15 minute break to participate also may have not shown up. This can create experimental error because it means we tested a smaller number of individuals, and less data means that our data is less close to normal.
Our second major concern was to where we would draw the lines on our population. The bias issue associated with this was that of convenience sampling. This issue produced bias because it was convenient for our lab group to simply choose from the individuals that attended "The Center" in the afternoon, rather than selecting from the entire "Center" population. We also could've tested individuals from other city schools, but that would be difficult to achieve. However, if we would've extended our experiment to outside of the junior and senior classes here at "The Center," we could've been able to create a larger, more randomized, and variant sample that would've made the data closer to normal or more believable. Since we stuck to the convenient population of the junior and senior classes at the center, bias was formed under the fact that our data were taken from a superior group of students and that the completion times might be faster since we at "The Center" may have better memories than those students found elsewhere.
Finally, concerning the validity of our experiment were the problems of achieving a truly random sample. During the two days we tested, some individuals weren't present to be tested on the day specified. So, some of these individuals came on different days to complete our memory game and thus they could've been switched from our silence first group to the music first group or vice versa. This would cause more individuals to be in a certain "block" over another, which happened to be that there were more individuals in our silence first group then in the music first group. However, the difference was only three individuals between the two groups and therefore our data wouldn't be skewed as much. Also, when selecting our 37 random integers for selecting certain people, it was very difficult to get the calculator to produce 37 different integers, but we finally achieved 37 different random integers from the random integer command on our calculator. We could've solved this problem though if we had gotten, say, 30 different integers, and then from the remaining 7 integers that we needed we could've randomly generated them one at a time.
Section 4: Findings and Analysis
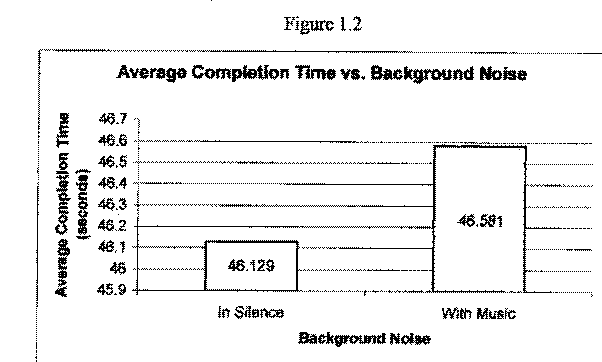
Figure 1.2 shows the average completion times for individuals completing the memory game in silence and with music in the background. As you can see in Figure 1.2, the average completion time with each treatment was approximately the same and thus we are led to the possible conclusion that there is no significant difference in completion times when an individual completes the test in silence or with music.
Next, in Figure 1.3 in the Appendices section, you can see the data of all the completion times for each individual when the memory game was completed in silence or with music in the background. The spread of the silence data, or the lowest and highest completion times within the treatment, was from 1 to 85 seconds with a center of approximately 40 seconds. Then, the spread of the music data found in Figure 1.3 is from 1 to 70 seconds with a center of approximately 46 seconds. These numerical descriptors provide us with the knowledge of how much variance there was present within our population. The knowledge of this variance allows us to see if there was a large difference in bias or variability which would allow us to more accurately conclude this experiment.
In testing for the significance of our data, we needed to use a matched pairs t-test which holds the formula of: t = (d-bar - μd) / (sd/√n). Also, I tested our data at α = .05. So, to begin the testing, there are the hypotheses that must be made, followed by the checking of the proper conditions, then the calculations, and then finally the conclusion based upon the calculations and hypotheses. This process goes as follows:
Hypotheses: Ho: μd = 0 or H1: μd > 0.
Conditions:
1. S.R.S.?
The population sample was chosen using an S.R.S. so the matched pairs t-test may be used.
2. Sample Size/Normality?
Sample size, n, is equal to 31 and since there are no outliers or strong indications of skewness we can test the data as being approximately normal.
Calculations:( value and standard deviation of difference can be found in Figure 1.4)
t= ( - μd) / (sd /√n)
t = (.452 - 0) / (16.095 / √31)
t = .452 /2.891
t=.156
degrees of freedom: df = 30
P-value (α = .05) = .9554
Conclusion: Fail to reject Ho.
After computing our data and arriving at the proper conclusion, we needed to further test for a 95% confidence interval in our conclusion. This is done using μd + E, where E stands for the error term which is found using E = t*(sd /√n). The calculations for the 95% confidence interval are as follows:
E = t* (sd /√n) {t* = 1.697}
E = 1.697 (16.095 / √31)
E = 1.697 (2.891)
E=4.906
CI: μd + E
CI: .452 + 4.906
CI: (-4.45. 5.36)
Section 6: Appendices
Figure 1.3
Individual |
Before (In Silence) |
After (With Music) |
Difference (After - Before) |
1 |
31 |
24 |
-7 |
2 |
36 |
39 |
3 |
3 |
38 |
51 |
13 |
4 |
38 |
58 |
20 |
5 |
36 |
15 |
-21 |
6 |
43 |
38 |
-5 |
7 |
50 |
45 |
-5 |
8 |
81 |
56 |
-25 |
9 |
25 |
63 |
38 |
10 |
35 |
49 |
14 |
11 |
69 |
59 |
-10 |
12 |
73 |
52 |
-21 |
13 |
59 |
70 |
11 |
14 |
40 |
52 |
12 |
15 |
63 |
40 |
-23 |
16 |
34 |
35 |
1 |
17 |
37 |
27 |
-10 |
18 |
31 |
50 |
19 |
19 |
40 |
57 |
17 |
20 |
85 |
62 |
-23 |
21 |
32 |
35 |
3 |
22 |
40 |
45 |
5 |
23 |
42 |
46 |
4 |
24 |
80 |
42 |
-38 |
25 |
40 |
47 |
7 |
Individual |
Before (In Silence) |
After (With Music) |
Difference (After - Before) |
26 |
34 |
39 |
5 |
27 |
53 |
61 |
8 |
28 |
30 |
33 |
3 |
29 |
50 |
57 |
7 |
30 |
46 |
55 |
9 |
31 |
39 |
42 |
3 |
Figure 1.4
Mean Difference () |
Difference Standard Deviation |
Sample Size (n) |
.452 |
16.095 |
31 |
Advanced Statistics Project #2
January 3,2005
Section 1: Introduction
The purpose of our project was to find out if students playing a game of memory would complete the game faster in silence or with loud noise in the background. The memory game consisted of fourteen playing cards (all of one color). The player had to match the different numbered cards with their corresponding match (for example, the eight of spades matched the eight of clubs). Each student was timed playing the game in silence and playing the game with loud music in the background. By comparing the differences between those two times and performing the necessary calculations, we can come to a conclusion on whether background noise is a factor when playing the game of memory.
We chose this topic because it could correlate to our own personal activities. if we discover that most students perform better with loud noise in the background, it may indicate that while performing other tasks, such as taking tests or doing homework, a loud atmosphere could actually be helpful. If our findings conclude that the majority of students had a slower time when playing the game of memory with loud noise in the background, we could infer that silence is better for students when they are taking tests or doing homework. Of course, oru results would only be based on playing the game of memory, but if our findings do indicate that background noise is very helpful or very unhelpful, it could lead to future experiments with test-taking, etc.
Before making our hypothesis, my group talked about how we studied or did homework best. It was discovered that all four of us worked better and got less distracted when there was little or no noise in the background. The game of memory does require concentration, so we thought that playing the game in silence would probably be easier for most people than playing the game with lots of noise in the background. Therefore, our hypothesis is that students will have better overall times when playing the memory game in silence than when playing the memory game with loud noise in their surroundings. This hypothesis makes sense because most individuals can concentrate better and perform more accurately when their environment is quiet and serene.
Section II: Study Design
The population in this experiment was the thirty-one randomly chosen Math and Science Center students. We assigned each junior and senior at the Center a number and then, using the random generator function on our calculators, generated forty numbers. We matched those forty generated numbers to the corresponding students and asked them to please participate in our project. Out of the forty students asked, thirty-one participated and played both versions of our memory game. These thirty-one students made up our sample.
Our experiment consisted of two versions of the classic memory game. Our memory game was comprised of fourteen different playing cards (all of the same color). In the fourteen cards, there were seven pairs. To play the game, the student would sit at a table where all fourteen cards were turned so you could not see what number they were. When the timer said "go", the students could flip over the cards, two at a time, until they found a match. Each match could remain face-up on the table. When the student had found all matches, they raised their hand, and their time was recorded.
Each student who participated in our experiment played the memory game twice. We randomly separated our population into two groups originally. Group A played the memory game in silence first, and then with loud oldies music on. Group B played the memory game with loud oldies music on first, and then in silence. We also had some students play the game with a red deck of cards and other students play the game with a black deck of cards. (Explanations for these experimental design decisions can be found on page five.)
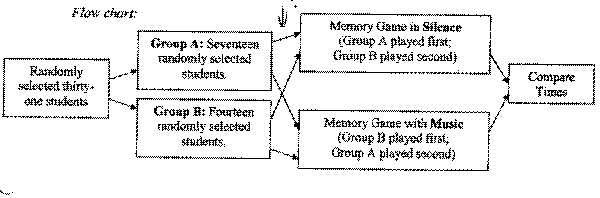
Section III: Design & Implementation Concerns
When planning our experiment, we had three major concerns. Our first concern was getting a truly random sample of students and enough students to participate in our experiment. Secondly, we did not want to create a game that would naturally be easier for some students to play. Almost all students have played the game of memory, but we had to take into consideration those that have never played it before. Additionally, we were apprehensive about students getting faster times the more they played the game. This would lead to results that wouldn't be related to noise level in the room. These three concerns had to be dealt with before we could begin our experiment.
We had some difficulties getting a truly random sample because not all of the students randomly chosen wanted to participate in our experiment. Also, some students that were chosen were sick on the day of the trials or had other commitments at the same time that we were playing the game. Ideally, we wanted forty students to play the game in both environments, but these restrictions only produced thirty-one students. This is acceptable for our experiment, but, as with all scientific experiments, the more data you collect, the more reliable your results will be.
Creating a fair game was another challenge. Before starting the game, we made sure that every individual understood the game so there would be no confusion of the rules. We also randomly directed the students to either a red deck of cards or a black deck of cards. This way, if students had a particular preference of which colored deck they played with, it was all randomized. If we hadn't chosen this way of playing the game, bias might have occurred. For example, if we had students play one game with a red deck and one game with a black deck, students with a preference (suppose they would more easily differentiate between clubs and spades than hearts and diamonds) would finish the game faster with their deck of choice. That way, the difference between the times of the two games would not be related to the surrounding atmosphere. Additionally, if we had just played the game with one colored deck (black or red) students with a preference would have an unfair advantage over the other students and we would not have a fair game.
The last challenge we had to face was the hardest to solve. Our group worried that the students' times of their second game would be better than then their times of the first game, regardless of atmosphere. We feared this would occur because students might get better at the game the more times that they played it. To solve this problem, we created Group A and Group B. By having Group A play the game in silence first and in music second and Group B play the game in music first and silence second, we reversed any problems that might have occurred. Even if students' times were better automatically the second time they played the game, the average differences between the two times wouldn't be greatly affected.
Section IV: Findings and Analysis
We compiled our data into a table and found the average time the game was played in when the room was silent and the average time the game was played in when the room was noisy (data and calculation on page 11). A comparison of these two average times can be seen in Figure One.
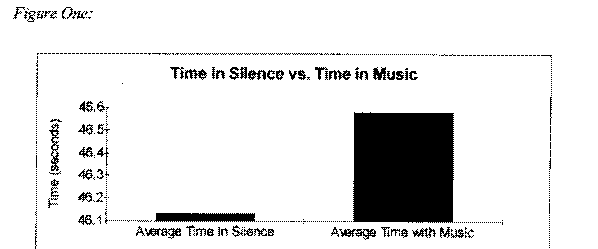
As you can see, the average time the game was played in when the room was silent is less than the average time the game was played in when the room was noisy. The average time in silence was 46.129 seconds while the average time with music was 46.58 seconds (calculations and data can be found on page 11). The average difference between a student's time in silence and their time in music was .452 seconds. This was not as big a difference as we expected to see.
The lengths of time that it took students to play the memory game varied greatly. Students playing the game in silence had times varying from 25 seconds to 85 seconds. Students playing the game with music had times varying from 15 seconds to 70 seconds. The differences between playing the game in silence and playing the game with music ranged from -38 seconds to 38 seconds. This is a very large range of time differences. The median (or middle value) of all the students' times while playing the game in silence was 40 seconds. The median of all the students' times while playing the game with music was 47 seconds. These values were calculated using the data on page 11 and our TI-83 Plus calculators.
Test of Significance
Our next step was to test the significance of our data. We used a matched pairs t-test and tested at an alpha of .05.
Hypothesis: Ho: μd = 0.
Ha: μd > 0.
Conditions:
1. Simple Random Sample? We selected our population using a Simple Random Sample so a matched pairs t-test may be used.
2. Sample Size? Our sample size is between 15 and 40 people (15 < 31 < 40), but we can assume that the data is approximately normal because there are not outliers or strong indicators of skewness in the data.
Calculations:
Matched pairs calculation (standard deviation and average difference found using calculators and data found on page 11)
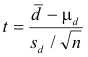
t = (.452 - 0) / (16.096 / √31)
t = .452 / 2.891
t = .156
P-value calculation
Degrees of Freedom = 30
P-value (α = .05) = .9554 (using our advanced statistics book)
Conclusion:
.156 < 1.645, so we fail to reject Ho.
Confidence Interval
After coming to our conclusion based on the calculations found on page 8, we needed to test for a 95% confidence interval. A 95% confidence interval will show us a range of values that our t statistic should be between in order to be 95% confident in our conclusion. If our t statistic is not between the two values found, our calculations would be incorrect at some point.
Error:
Error = t* (standard deviation / square root of sample size)
To find t* we looked in Table C of our Advanced Statistics Book (1.697)
Error = 1.697 (16.095 / √31)
Error = 1.697 (2.8910)
Error = 4.906
Confidence Interval:
Confidence Interval = mean + E
Confidence Interval = .452 + 4.906
Confidence Interval = (-4.454, 5.358)
Conclusion:
-4.454 < 0 < 5.358, so we can say that we are 95% confident in failing to reject Ho.
Section V: Conclusions & Study Limitations
We found that there was no significant difference in the amount of time it took to play the game of memory in silence and the amount of time it took to play the game of memory with loud noise in the background. Although our results did show that it took an average of .452 seconds longer to play the game with music on, this is not a significant amount of time. We came to this conclusion by performing the matched pairs t test and by finding the 95% confidence interval. After completing those tests, it was apparent that, at α = .05, there is no difference in the time it takes to play the game in silence and to play the game with music on.
Our hypothesis was incorrect for this experiment. We had originally thought that the amount of time it took to play the game with loud background noise would be significantly more than the amount of time it took to play the game in silence. We can then infer that most students at the Math and Science Center can concentrate either in silence or with activities going on around them. Our data did not lead us to think that either a silent room or a loud atmosphere was better for playing the game of memory. Therefore, our hypothesis was proved incorrect.
There are some design flaws that may have altered our outcome. Our sample size was not as large as we would have liked. As mentioned before, a larger sample size would have resulted in more accurate data. After reflecting on the game, I also came to the conclusion that a game with more matches may have produced better data. Our game may have been too simple for the students at the Math and Science Center. If we would have had more cards that they needed to match, it is possible that we would have seen a greater difference between the students' times in silence and their times in music. Lastly, I believe that more noise or a louder music choice would have been better. When we were performing our experiment, other classes were also being held so the noise level could not be as high as we would have liked. If there was more distraction to the students, we may have seen a different outcome.
In conclusion, our experiment found that there is no significant difference between the time is takes to play the game of memory in silence and the time it takes to play the game of memory with music on. We are very confident in our conclusion after performing the various required tests.
Section VI: Appendix
Data Table
Individual |
Before (silence) (s) |
After (music) (s) |
Difference (s) |
1 |
31 |
24 |
-7 |
2 |
36 |
39 |
3 |
3 |
38 |
51 |
13 |
4 |
38 |
58 |
20 |
5 |
36 |
15 |
-21 |
6 |
43 |
38 |
-5 |
7 |
50 |
45 |
-5 |
8 |
81 |
56 |
-25 |
9 |
25 |
63 |
38 |
10 |
35 |
49 |
14 |
11 |
69 |
59 |
-10 |
12 |
73 |
52 |
-21 |
13 |
59 |
70 |
11 |
14 |
40 |
52 |
12 |
15 |
63 |
40 |
-23 |
16 |
34 |
35 |
1 |
17 |
37 |
27 |
-10 |
18 |
31 |
50 |
19 |
19 |
40 |
57 |
17 |
20 |
85 |
62 |
-23 |
21 |
32 |
35 |
3 |
22 |
40 |
45 |
5 |
23 |
42 |
46 |
4 |
24 |
80 |
42 |
-38 |
25 |
40 |
47 |
7 |
Individual |
Before (silence) (s) |
After (music) (s) |
Difference (s) |
26 |
34 |
39 |
5 |
27 |
53 |
61 |
8 |
28 |
30 |
33 |
3 |
29 |
50 |
57 |
7 |
30 |
46 |
55 |
9 |
31 |
39 |
42 |
3 |
Average |
46.129 |
46.58 |
.452 |
To find the average:
Sum(all before times)/31 = average of before times
Sum(all after times)/31 = average of after times
Sum( all difference times )/31 = average of differences between after and before times
Tape Brand Comparison for Stickiness
Advanced Statistics
May 23, 2003
Section 1: Introduction
When one purchases a product in stores today, he or she is often faced with the question of whether to buy the slightly more expensive brand they recognize or the less expensive brand that they have never heard of. Certain brands were put in the spotlight years ago for being known as high quality and innovative. However, in present times the quality of these name brands has come under scrutiny. Many name brand companies have been known to cut quality without cutting the price in order to make a more substantial profit. One of the most recognizable brand names is Scotch®. Often the transparent adhesive tape, used for everything from hanging posters to wrapping Christmas presents, is not even called transparent tape anymore but rather "Scotch Tape."
The purpose of this experiment is to determine if Scotch® tape can hold as much weight as a basic generic brand purchased from Walmart®. This generic tape did not even display a brand name and was simply labeled "Transparent Tape." It is my hypothesis that the generic brand tape will in fact be able to support more weight than the Scotch® brand tape.
Section 2: Study Design
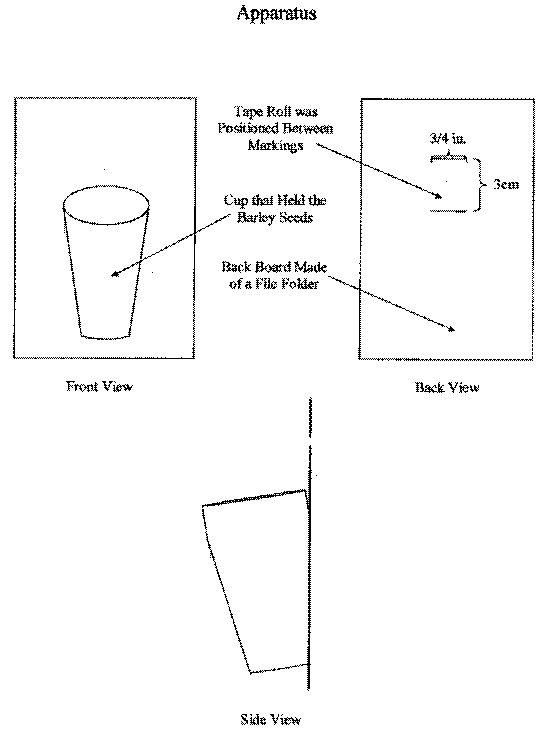
Since it is impractical to test the entire population of Scotch® tape and the generic tape that we chose, we decided to take a sample of fifteen pieces from each brand of tape. While taking simple random samples of the entire populations is ideal, it is impractical. Instead we used one roll of each brand of tape and took a piece of tape from the end of fifteen three-foot increments for each roll, as seen in Figure 1. This was to create as random a sample as possible while taking into account that the stickiness of the tape may increase or decrease the closer you are to the center of the roll of tape.
Since the amount of weight that a piece of tape can hold is dependent upon the surface area
of the tape that is being tested, we decided to use a grid and measured the tape so that when it was
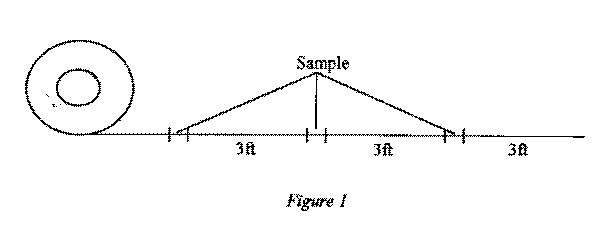
rolled the surface area measured 3/4" by 3cm on each sticky side. The side of the tape roll that was adhered to the grid was always the side that was adhered to the apparatus that we built to test the tape. In order to compare the maximum weights that Scotch® tape and the generic brand can hold, we must maintain a level of control. In order to do this we constructed a single apparatus (see Appendix A) that would be used with both brands of tape. The apparatus was marked on the back where the tape would be adhered and, likewise, the wooden door to which the tape and the apparatus was adhered, was also marked to ensure the tape was positioned in the same location for each trial. In addition to this, the trials were alternated between tape brands. First we tested the Scotch® tape, then the generic brand, then the Scotch® tape, and so forth. This was done to lessen the effects of any sticky residue that may remain on the apparatus or the door after each subsequent trial.
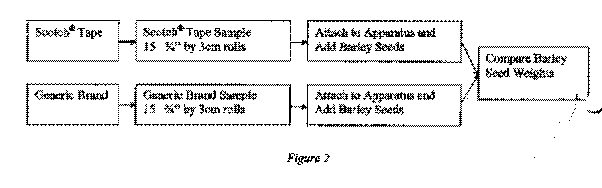
When deciding how to determine the weight that the tape could hold, it was necessary to find objects small enough to detect slight differences. Barley seeds were agreed upon as simple and easy objects to add and weigh. The barley was added to the apparatus until the apparatus completely detached from the door, then was poured into measuring trays and weighed on a scale. These measurements were added to the weight of the apparatus and recorded as the maximum weight that the tape could support. Figure 2 below shows a simple diagram of this experiment.
Section 3: Design and Implementation Concerns
While many precautions are taken to avoid the introduction of bias to our experiment, it is inevitable that there were design flaws and a certain degree of bias. For example, the initial sampling technique we outlined may systematically favor one brand of tape. The generic brand tape comes in a roll that contains approximately 1,500 inches of tape while the Scotch® tape contains much less. One of our concerns is that the tape may be less sticky or stickier towards the center of the roll. Our sanlpling process lessened the effects of this but did not completely eliminate the associated bias. It is still possible that the tape towards the outside is stickier or less sticky resulting in tape that is systematically stronger or weaker for the generic brand since the Scotch® tape is sampled from nearer the center of the roll.
It is also a concern that all of the samples of tape from each brand were obtained from only one roll of tape. It is possible that one of the rolls was defective. However, in this experiment we are forced to assume that each roll of tape is an accurate representative of its respective population.
In addition to this, during the experiment it was difficult to keep the speed at which the barley was added to the apparatus constant. It is possible that after the initial trial, the following outcomes were expected so that the barley was added at a faster speed in anticipation of the apparatus falling. A faster speed could present a stronger force being applied to the apparatus, which would result in a lesser amount of weight that the apparatus could hold. Since the rate that the barley was added was then slowed down when the anticipated time the apparatus would fall was approaching, it is possible that the way the barley was added systematically contributed to outcomes.
Section 4: Findings and Analysis
The data obtained for the generic brand tape produced a mean of 183.09, a minimum value of 152.48, Q1 value of 176.41, a median value of 184.17, a Q3 value of 191.77, and a maximum value of 206.77. Each of these values was greater than those produced from the Scotch® tape data. The Scotch® tape data produced a mean of 81.55, a minimum value of 69.15, Ql value of 75.82, a median value of 79.94, a Q3 value of 90.82, and a maximum value of 98.38. As can be seen in Figure 3, the minimum weight at which the generic brand fell was 54.1 g heavier than the maximum weight at which the Scotch® tape fell.
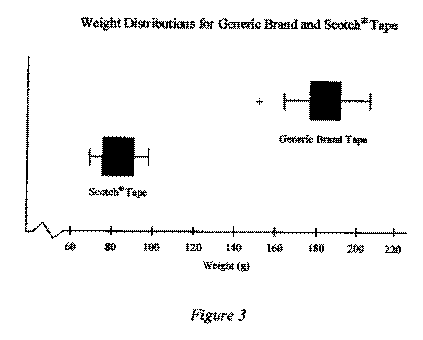
The data of the generic brand does appear to contain one outlier at 152.48, but as can be seen in Figure 4, this did not appear to skew the data significantly. The Scotch® tape data did not appear to contain any outliers and was not significantly skewed, though it did appear slightly bimodal as can be seen in Figure 4. The standard deviation of the generic brand data was approximately 13.036 and the standard deviation of the Scotch® tape data was approximately 9.016. The data for both the generic brand tape and the Scotch® tape can be found in appendix B.
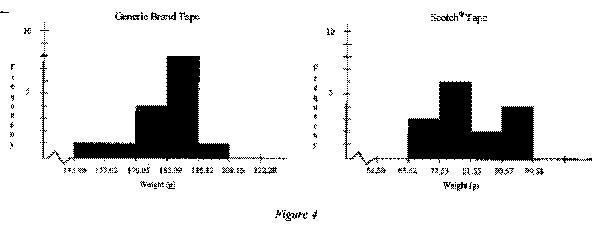
In order to complete a test of significance when comparing two samples from two distinct populations, two conditions must first be met. First, the samples must be simple random samples. In this experiment, neither of the samples of tape that were chosen were simple random samples. Second, the data that was received must give indication that the two populations in question are normally distributed. For this experiment, the population of generic brand tape can be considered approximately normal in spite of the outlier at 152.48, due to the fact that the histogram of the data appears approximately normal. The sample data for the Scotch brand tape did not give any indication that the population was not normal. The data was not significantly skewed despite the slight bimodal distribution nor were any outliers identified. We will proceed with caution.
Ho: μG - μS = 0. The mean weight that the generic brand tape is able to support is equal to the mean weight that the Scotch® tape is able to support.
Ha: μG - μS > 0. The mean weight that the generic brand tape is able to support is greater than the mean weight that the Scotch® tape is able to support.
degrees of freedom = n - 1 =15 - 1 = 14 degrees of freedom
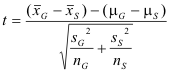
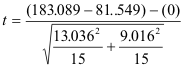
t = 24.814
p(t > 24.814) < 0.0005
We would expect an outcome as extreme as ours less than five times in ten thousand if Ho were true, so we have very strong evidence to reject Ho and conclude that the mean weight that the generic brand tape is able to support is greater than the mean weight that the Scotch® tape is able to support. However, since only one of our conditions was met, the validity of our conclusion is questionable.
In order to calculate a confidence interval when comparing two samples from two distinct populations, the same two conditions must be met in order to complete a test of significance. As stated above, neither sample is a simple random sample, but both populations may be assumed normal despite the outlier in the generic tape data because the distributions appear approximately normal. We will proceed with caution.
degrees of freedom = n - 1 = 15 - 1 = 14 degrees of freedom
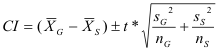
CI = [92.763, 110.317]
If multiple confidence intervals were constructed from repeated simple random samples of the population, 95% of them would contain the difference in the mean weights that the population of generic tape and the population of Scotch® tape are able to hold. However, since only one of our conditions was met, the validity of our conclusion is questionable.
Section 5: Conclusions and Study Limitations
Based on the results of this experiment, I will accept my hypothesis that the generic brand tape is able to support more weight that the Scotch® tape.
The bias introduced due to the different roll sizes may have significantly affected this experiment. If tape progressively becomes less sticky as it gets closer to the center of the roll, the generic tape samples may have been stickier simply because they were closer to the outside of their roll than the Scotch® tape samples were. However, neither set of data appeared to give any indication that the first samples were systematically greater than the later samples.
During the experiment, the trays used to hold the barley were not large enough to hold enough barley to make the apparatus fall. Therefore, when filling the apparatus it was necessary to switch trays in the middle of each trial several times resulting in a longer period of time the apparatus was held to the wall with the tape. This time lapse could have significantly lessened the amount of weight the tape could hold. However, it is not apparent that there was any systematic trend to the amount of barley present in the trays in relation to the brand of tape being tested.
It is my opinion that the results we obtained during this lab are significant based on the results of the test of significance and the confidence interval. Both tests showed that the difference in mean weight that the apparatus could hold was significantly different for the generic tape than the Scotch® tape. It is unlikely that the speed at which we were adding the barley would cause such a significant difference. However, as addressed before, in order for these results to be valid, one must assume that the rolls of tape are accurate representatives of their respective populations.
Appendix A
Appendix B
Trial |
Generic Brand Weights (g) |
Scotch® Tape Weights (g) |
1 |
206.77 |
71.84 |
2 |
191.77 |
98.38 |
3 |
163.90 |
77.19 |
4 |
183.98 |
76.37 |
5 |
184.17 |
92.33 |
6 |
176.37 |
69.15 |
7 |
176.41 |
81.15 |
8 |
177.21 |
79.94 |
9 |
182.67 |
90.82 |
10 |
185.05 |
84.77 |
11 |
186.93 |
75.82 |
12 |
192.19 |
75.85 |
13 |
152.48 |
92.40 |
14 |
191.65 |
70.09 |
15 |
194.78 |
87.14 |
Critical Research Concerns and Report Style Guide for Research Papers Jeffrey V. Bohl, Battle Creek Area Mathematics and Science Center |
About the Study
Defining your population
First, the sample needs to be from the population. If your sample is from several boxes of Oreo cookies, then your population is not all cookies. It might be all Oreo cookies, or only Oreo cookies from the same manufacture batch as the ones you bought. This is not a problem (so don't discuss it as a concern in your study), it just means that your study is only about all Oreo cookies and not all cookies.
About study concerns
BIAS is the big problem you need to be worried about. Remember that bias results in your data systematically favoring certain types of outcomes. This, in turn, makes your statistic ( or DIFF) not representative of your actual population. When you have a study concern, you need to note specifically what the potential bias issue is.
Here are some examples that might clarify this. Read them carefully:
Example 1 (Bias): Say your population is all juniors and seniors at the BCAMSC. Because you were too lazy to take a real SRS, you picked every 3rd person to come into MPR during lunch. This could cause bias because the pool of people you actually chose from (students who arrive early at school) might be the type of people who are more likely to (a) enjoy being in school more (b) be from particular home schools that are closer to BCAMSC and might therefore share some characteristics with each other more than they do with other students, or perhaps (c) have more free time on their hands generally than does the general population of juniors and seniors at BCAMSC. This is bias because those types of people are over-represented in your sample. You need to note it as a potential problem and say why it's a potential problem.
Example 2 (Maybe bias): Say your population is two boxes of different brands of cookies. In your experiment, you drop cookies into a cup of milk to see how long they float. Your cups are a little small, though, and some cookies float against the side and cling there, greatly increasing the floating time. This could be bias or not, depending on how you define the problem.
If you are studying "the differences in floating times between Brand-X and Brand- Y cookies in small cups of milk," then there is no bias here. Even if Brand-X cookies were more likely, for some reason, to cling to the sides of the cup, that is simply one of the reasons they float longer. Since you state in the problem that you are studying only small cups, and you are not making any
claims about why a cookie might float longer, then there is no problem. There is no bias. You need not note it as a problem.
If, however, you are studying "the differences in floating times between Brand-X and Brand- Y cookies in milk," the clinging problem does introduce bias, because the cup size should not be a factor. When you use the small cup, you are systematically favoring the brand that is more likely to cling. This is bias. You need to note it and explain the potential problem in terms of the bias concern it introduces.
Also, if you were simply studying "floating times of Brand-X in milk," there would be a bias concern for the same reasons, since the cup-clinging issue factors in and it should not.
About maintaining control
Control is not only having a control group. Control is the concept of doing all you can to keep all variables constant except the one you are studying. Thus, there are many, many ways in any experiment that you ought to work to maintain control. Here are some examples:
Example 1: A study involving a survey
We made sure that all the surveys looked exactly the same, and had the questions in the same order. All participants took the survey while sitting alone in the library to minimize distractions. Each participant was asked, using the exact same wording, "Would you please take 3 minutes to fill out this survey about your activities outside of school. It's for my Statistics class, and it would be a great help to me if you would take it. Thank you in advance for being honest." This helped make sure that each person went into the survey with the same understanding of what it was. Each person was given only 3 minutes, at which time they were asked to stop.
Example 2: Bouncing balls
In the experiment, we dropped the balls from a height of 42 inches as measured with a yard stick. The same person dropped the ball each time to ensure consistent release, and the same person noted the height of the bounce back up to help maintain consistency. Before taking the actual measurements, we practiced dropping the ball and measuring the height so that we had developed consistency ahead of time. Also, the ball was dropped on the exact same cement surface in approximately the same spot for each trial to make sure that differences in surface would not affect the bounces. All trials were conducted within 30 minutes of one another to help control for potential changes in temperature in the room and the balls.
About data collection tools (tests, surveys, etc.)
Be sure to include any of these as appendices. They help the reader understand exactly what it is you did.
About Report Contents and Format
Assumptions of reader knowledge
Be sure that you give full descriptions of the experimental design. Do not assume that the reader knows anything about the experiment you did.
Graphs, Diagrams, and Tables
Here are some general hints and rules for the use of graphs and tables.
1. Each graph and diagram should be named, in order, "Figure 1", Figure 2", and so on. The name of the figure and a description of it should be underneath the graph and left aligned, like this:
2. Each table should be named, in order, "Table 1", Table 2", and so on. The name and description of the contents of the table should be formatted as above for figures.
3. Each figure or table must be referred to by name in the body of the paper. Do not just put
a figure or table in without referring to it and describing what it is.
4. Never have a graph or table be the first thing in a section of the paper. Always begin a section with some text.
5. If you have two or more graphs that you want the reader to do visual comparisons between, it is critical that the axes have the same scales with the same ranges of values shown.
6. If you have many values to report, consider putting them in a table as well as describing them. It is easier for the reader to follow multiple comparisons if there is a table containing the numbers.
7. If you want to show what a distribution of data looks like, either frequency histograms or boxplots are appropriate. Bar charts are not appropriate for measurement variables.
8. Do not connect dots on a scatterplot unless there are values between the dots. In general, unless you are doing a regression study, you should not be using scatterplots.
Project #3 – Observational Study and Analysis
Noakes A.P. Statistics – 2004/2005
(Adapted from Jeff Bohl)
Project Objective
The end goal of this project is an 8 – 12 page paper in which you report the results of an observational study that you design and implement, and an analysis of the results. The study must be designed and reported within the parameters given below. The goals of this project are:
1) To give you experience in observational study design and implementation, and
2) To give you experience doing statistical inference in the context of an observational study.
Keep this in mind as you do your write up: It is important that you make clear your knowledge of the important issues of study design, and the strengths or weaknesses of your particular design. You will not be graded down too much for not having a perfect study. However, you will be graded down a lot if you fail to specify how your study is imperfect and what the implications of the imperfections are for your results.
Study Topic (See Attached Sheet)
You must work with data in which you can compute a mean or a proportion for your sample. I must approve your study design before any experiments are done. (See the attached approval sheet.) You also must make a hypothesis (that can be tested with a significance test) concerning the relationship you expect to find between the two populations.
Study Design
The study must be designed in such a way that its implementation:
a) Provides as nearly a simple random sample as possible.
b) Requires the use of a sample from each of two independent populations.
c) Provides an n ≥20 for each group.
Analysis
You will do inference on μ or p two different ways:
1. You will do a test of significance for your initial hypothesis comparing your two sample means (this is a test on two means) or a test of significance for your initial hypothesis comparing your two sample proportions (test on two proportions). You can do either a one- or a two-tailed test depending on which is appropriate.
2. You will create a confidence interval for the difference between the two populations.
Grading
This report will be worth 150 points. It will be graded on two sets of criteria. 20 points will be based on the format and neatness of the report, 30 points on the study design, and 100 points on the thoroughness of your descriptions of the design, implementation, inference, and conclusions. The report must be formatted and contain all information as described on the next page.
Report Requirements
Format and Style
All of the text in your report must be typed double-spaced. The report must contain the following:
a) A title page.
b) Separate sections entitled as noted below which meet all of the listed requirements.
c) An Appendix with a copy of the data collection tool, all data, and a list of works cited.
Section 1: Introduction/Research Review (2-3 pages)
Begin with a statement of the topic of study. Be sure to note why this topic is interesting or important. Then find published research on the topic. You should be looking for results that have already been found by others. (Example – if you are conducting a survey on percentage of people who feel abortion should be illegal, find research that gives national percentages or other data. When were the studies done? What did the researchers find? (Be sure to include citations for all referenced material!) Then give a brief statement of what you are looking to find in the study. Do you expect that your results will be similar or different? Why? Finally, you should clearly state your experimental hypothesis.
Section 2: Study Design (1-2 pages)
Here you must accomplish several things:
a) Describe the question your experiment is trying to answer and your population of interest.
b) Describe the treatments.
c) Describe your method of sampling and explain specifically how it addresses concerns about randomness as well as the other requirements for the test of significance and the confidence interval.
Section 3: Design and Implementation Concerns (1-2 pages)
Describe any concerns you have about the methods by which you carried out your experiment. If there were any possible sources of bias, or any problems with getting a truly random sample, these must be noted here.
Section 4: Findings and Analysis (3-5 pages)
Give the results of your study. That is, report your μ or p values. Refer to the actual data, which will be included as Appendix 1. Also, provide a graphical representation of your data. Here you are to:
a) Do a test of significance on difference of means or proportions -- be sure to write hypotheses and conclusions both symbolically and in words. Use precise wording for the conclusion.
b) Create a confidence interval for m -- be sure to state the precise way that the confidence interval should be interpreted.
You must include ALL of the necessary calculations and enough explanation so that someone with a strong math background but no prior knowledge of statistics can read and make sense of them. Be sure to state the results of the test in a full, precise way.
Section 5: Conclusions and Study Limitations (1-2 pages)
Comment on the results of your test and C.I., making clear what the numerical results mean in terms of the context of your population and the question you asked. If your test shows a significant difference, you should state any reasons you believe that might be true. If your test shows no significant difference, you should clearly state that.
Be sure to state clearly what the limitations of this study are. This will include some statement about the limited nature of your population, concerns about the fact that your parameter is not actually from your target population, and any concerns that arose in your study design or sampling method that might make your conclusions less valid.
Section 6: Appendix 1
Here include, on a separate page labeled at the top, Appendix 1. This should consist of a copy of the data collection tool and the results of your survey. Be sure to also include a list of works cited (bibliography).
Project #3 – Rubric Name: _______________Adv. Statistics/A.P. Statistics
Format and Neatness |
All text typed |
(3) ______ |
|
_____/20
|
Symbols computer generated and correct size |
(4) ______ |
|
Graphics computer generated and clear |
(6) ______ |
|
Figures and tables labeled and referred to in text |
(3) ______ |
|
Title page/ 12 pt font, 1.5-2 spaces per line |
(4) ______ |
|
|
|
|
_____/30 Quality of Observational Design |
Utilizes randomization at every possible step |
(10) ______ |
|
Maintains as much control as possible |
(10) ______ |
|
30 experimental units minimum |
(5) ______ |
|
No Bias |
(5) ______ |
|
|
|
Quality of Written Report |
|
|
|
Statement of the topic |
(2) ______ |
|
_____/100
|
Why topic is interesting |
(2) ______ |
|
Review of published statistics/research on topic – including citations! |
(8) ______ |
|
Statement & Justification of hypothesis |
(3) ______ |
|
|
|
|
Section 2: Study Design (1-2 pages)how control was maintained |
|
|
Identify both populations clearly and correctly |
(2) ______ |
|
Describe observational study & data collection |
(5) ______ |
|
n ³ 30 (at least 15 in each sample) |
(2) ______ |
|
Complete description of survey questions |
(2) ______ |
|
|
|
|
Section 3: Design & Implementation Concerns (1-2 pages) |
|
|
Correct identification of major concerns (confidentiality, questioning bias, truthfulness of responses, etc.) |
(5) ______ |
|
Explanation of bias issues related to each concern |
(5) ______ |
|
Problems getting truly random sample |
(3) ______ |
|
|
|
|
Section 4: Findings and Analysis (3-5 pages) |
|
|
Data in graphical form |
(3) ______ |
|
Describe and compare for each sample |
(3) ______ |
|
Comment on each figure or table |
(3) ______ |
|
Specific numeric descriptors of spread and center (if applicable) |
(3) ______ |
|
Reference to actual data in appendix |
(3) ______ |
|
Test of significance |
|
|
Appropriate procedure |
(3) ______ |
|
Conditions checked |
(5) ______ |
|
Proper cautions noted if conditions not satisfied |
(3) ______ |
|
t statistics calculated appropriate (formula shown) |
(3) ______ |
|
P-value found with df reported |
(3) ______ |
|
Conclusion correct based on P-value |
(4) ______ |
|
95% Confidence interval |
|
|
t* identified correctly |
(3) ______ |
|
Interpretation/conclusion correct |
(5) ______ |
|
Final Grade ______/ 150
|
|
|
|
Section 5: Conclusions and Study Limitations (1-2 pages) |
|
|
Correct statement of conclusions regarding study |
(5) ______ |
|
Reference to hypothesis |
(3) ______ |
|
Full statement of how design flaws affect conclusions |
(3) ______ |
|
|
|
|
Section 6: Appendices |
|
|
A: Table of all data |
(2) ______ |
|
B: Data collection tool |
(2) ______ |
|
C: Bibliography |
(2) ______ |
Observational Study: Knowledge of Current Events vs. Political Affiliation
Advanced Statistics
Mrs. Noakes
January 18th 2005
Introduction
Politics should be on the mind of every American. Each American should know about their government. They should know at least a little about bills that are being passed that may affect them. They should make educated decisions about what political candidate to vote for every four years. These things should take place but it seems that more and more people in the United States have no idea what is going on in the government that rules them. In fact “When it comes to politics, Americans who don’t know what they’re talking about have a lot of company. [They] represent a majority of voters”.(Sullum, 2004) Our observational study targets this problem and strives to answer the question “does knowledge of government and current events depend on political affiliation?” We will conduct a survey in our local area to see which of three political parties (Republican, Democrat, and 3rd Party) has the most thorough knowledge of current events.
The range of people affected by our study and other studies of this type is very extensive. The fact that the government makes decisions that affect every American’s life, each American can learn something from our results and possibly realize that they must pay more attention to their government. Younger people or people that are not able to vote may learn something about how their country works and be able to make an educated choice when they are able to vote. Older people who are able to vote may be forced to think about the position of their supported political candidate and possibly open their eyes to a candidate that has the same feelings as they do. Political officials can also use the results of these surveys to see how knowledgeable the public is in terms of their policies. This may lead to more campaigning and more focus in making the public aware of where they stand.
These examples of how our survey could be used by others. We picked this topic of study because of our strong beliefs in American politics. Our group often talks about what is wrong about the government but we are too young to vote (me by only months) we look for other ways to show the American public that they are not giving enough thought to their ruling body. The definition of democracy is “a form of government under which the power to alter the laws and structures of government lies, ultimately, with the citizenry. Under such a system, legislative decisions are made by the people themselves or by representatives who act through the consent of the people, as enforced by elections and the rule of law.”(Wikipedia.com) The form of democracy in the United States is that of elected officials and not that of all of the people. Citizens in America find it sufficient to elect, often times blindly, officials which they think will make good decisions. Sometimes there is not enough care taken in the election of officials and sometimes unfit officials have been elected.
Several studies have been done that have to do with the idea of knowledge of the people as a whole and knowledge of separate factions of the people. One of these studies was conducted by the Program on International Policy Attitudes during mid-September. This study claimed that most supporters of George W. Bush could not identify the policies of their candidate while supporters of John Kerry were able to show a more extensive knowledge of their candidate. Another example is an article posted on reason.com that showed examples of the huge lack of current events knowledge of United States citizens. Some of these examples are listed below:
In April 2004, 58% of Americans said they knew “little” or “nothing” about the USA PATRIOT ACT.
A month and a half after Congress passed the partial birth abortion ban, 65% of Americans did not know about it.
In a February 2004 survey, 60% of Americans responded to a survey claiming they did not know that Bush’s domestic spending had contributed to the rising federal deficit.
Another survey by the PIPA, conducted during October, found that three of four (or 75%) of Bush supporters believed that pre-war Iraq had weapons of mass destruction and connections to al-Qaeda. Both of these assumptions have been found to be false. The government stopped the search for Iraqi weapons of mass destruction after the election (on January 12, 2005 – Washington Post). The alleged connections between Saddam Hussein and al Qaeda were proven untrue in the final report of the bipartisan 9/11 commission. Supporters of George Bush had obviously victims of political propaganda, the same propaganda that rallied so much U.S. support for the “invasion” or Iraq. We hypothesize that out of the three political parties surveyed (Democrats, Republicans and 3rd party members), the Democrats will be the most knowledgeable of current events. Members of 3rd party groups will be the second most knowledgeable while Republicans will come in last. We base this hypothesis on the information we have gathered that shows that Democrats have a greater knowledge of the world around them than the Republicans. We did not find much information on 3rd party politics so we have put them after Democrats but before Republicans in current events knowledge.
Study Design
There are three populations present that we will be testing. One population is all of the people who identify with the Republican Party that vote in the United States. The next is all people who identify with the Democratic Party that vote in the United States. The last is all 3rd party members that vote in the United States.
The aim of the observational study and the use of our survey is to gauge the amount of current events knowledge of voters in America. We have created a current events test that is ten questions long that will help us get a numerical value of that knowledge that can be easily compared between groups and individuals. The number of correct questions on our survey will show how knowledgeable the person is.
We used a method called convenience sampling to administer our study. We gave out the quizzes at libraries, stores, restaurants and even schools in our local area. We asked random people in these establishments to take our survey. No one was forced to take the survey and non-response was a factor on several occasions.
Though we had several flaws in the sampling process, we avoided several types of bias in the way that we set up the study. First, we had a sociology major look at the quiz questions and eliminate any questioning biases. Second, confidentiality was kept by keeping names off the surveys and sealing the surveys in an envelope from the time of completion to the time of scoring.
We tested 68 total people and the breakdown of party affiliation is thus:
26 Democrats
21 Republicans
21 Members of a 3rd Party
As is shown in the appendix, the survey consists of questions with topics ranging from knowledge of geography to knowledge of the current administration to foreign governmental affairs. Also included are questions having to do with the UN and our own US government
Design and Implementation Concerns
Several of our sampling methods and possible opportunities for bias must be thought over before the actual study can take place. These include:
SRS vs. Convenience Sampling
Non-response
Non-compliance (cheating)
The first problem we encountered with out study was getting a simple random sample. This, in our case, is nearly impossible with the resources we have. To get a simple random sample of all of the target voters in the United States, we would have to have detailed voter registration lists. This is something that I am convinced we would not be able to get. And even if we did, the daunting task of contacting so many people across the US would take too long for a group of four high school students. We accepted this and used convenience sampling instead. We picked random people at libraries and other locations but this stopped us from getting an accurate sample of the possible voting population. We had a problem when we tried to salvage something of an SRS by going to the mall and getting random passers by to take the survey. We were not allowed to give them out because of the “stress” they would have caused shoppers during the holidays. Therefore we were in a way forced to conduct convenience sampling. We did the best we could with the resources we have been given and in my opinion the lack of an SRS on our particular study on the scale that we conducted it on should not have been too much of a problem.
We did have several cases of non-response when handing out surveys. Some people refused to take the quiz and even though this did not happen often, it is possible that one of the political parties was more reluctant to take the quiz and therefore our data for that party is not correct. We had several cases of cheating on the surveys that forced us to throw out one or two of the surveys. We do not think that this affected our data to a crippling degree but this must be mentioned nonetheless.
Findings and Analysis
The first graph below is a histogram of the overall data. The mean score on the test is shown for each overall political group. These average scores will be used later in many of the calculations.
Figure One: Test Score Averages
By looking at the histogram, we can see that the third party members on average answered the most correct questions on the quiz while Democrats came in second and Republicans were last. The average for the third party is a little over 7 while the Democrats came in at just under 7 and the Republicans were in last with a little under 6 correct answers. This can’t be considered the results of the lab as we still have calculations to make to find the significance of the differences in quiz scores.
Figure Two: Democrat Scores Detail
This histogram represents distribution of the Democrat scores we got in the study. The distribution is skewed left and has an average or middle around 7. There is an average amount of spread in this distribution.
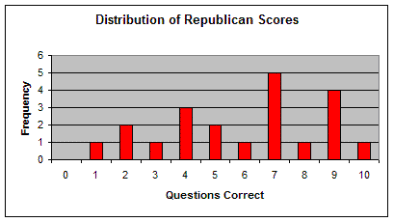
Figure Three: Republican Scores Detail
The data for the Republicans is more spread out than that of the Democrats. It is only slightly
skewed left and has a middle or mean around 6.

Figure Four: Third Party Scores Detail
The distribution for the third parties is by far the least spread out of the groups. It is strongly skewed left and has a middle or mean around 7.
By looking at the histograms, we can already begin to make guesses about what the most knowledgeable party will be. We can’t make any decisions until we do significance tests like the ones shown below.
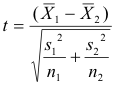
We decided to do three significance tests using two sample t tests. We used the formula
to calculate the t value which we then used to find if the occurrence of such an event was purely due to chance or not. We used the formula
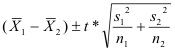
to calculate the confidence intervals.
![]() is the mean of the Democrats’ scores,
is the mean of the Democrats’ scores,
![]() is the mean
of the Republicans’ scores, and
is the mean
of the Republicans’ scores, and
![]() is the mean of the third party scores. Below are the results of the
significance tests. Note that
is the mean of the third party scores. Below are the results of the
significance tests. Note that
![]() refers to a sample mean, s refers to a sample standard deviation and
n refers to the number of units in a sample.
refers to a sample mean, s refers to a sample standard deviation and
n refers to the number of units in a sample.
Several conditions must be met for the two sample t tests to be valid. There must be a simple random sample and the data set has to be large. We must proceed with caution with the results of the study, as the second condition is met, but the first is not (the sample uses convenience sampling and is not an SRS). We are going to let α = 0.1 for the calculations.
Democrat vs. Republican
H0: m1 = m2
Ha: m1 > m2
We used the above equation (our calculator) to get the data:
t = 1.173
df = 42.0
p =.124
Because p > a, we fail to reject H0.
Democrat vs. Third Party
H0: m1 = m3
Ha: m1 < m3
We used the above equation (our calculator) to get the data:
t = -.446
df = 45.0
p = .329
Because p > α, we fail to reject H0.
Republican vs. Third Party
H0: μ2 = μ3
Ha: μ2 < μ3
We used the above equation (our calculator) to get the data:
t = -1.63
df = 37.45
p = .0555
Because p < a, we reject H0.
Now that we have these we can make confidence intervals to show what we think the actual difference between the values of the means is. We will use the confidence interval equation above. We will use Table C in our stats textbook to find t*.
Democrat vs. Republican
df = 42 (rounded down to 40)
t*= 2.021
(-2.433, -.6457)
We are 95% confident that the actual difference between the means of the Democrats’ score and the Republicans’ score is within the interval above.
Democrat vs. Third Party
df = 45 (rounded down to 40)
t*= 2.021
(-1.638, -1.046)
We are 95% confident that the actual difference between the means of the Democrats’ score and the third party’s is within the interval above.
Republican vs. Third Party
df = 37.45 (rounded down to 30)
t*= 2.042
(-2.666, -.2860)
We are 95% confident that the actual difference between the means of the Republicans' score and the third party’s score is within the interval above.
Conclusion and Study Limitations
This study, due to the fact that we used convenience sampling, was a hard one to take seriously. The results say something but the fact that we said proceed with caution kind of takes away from the authenticity of the results. Only one conclusion can be made from looking at the two sample t tests. This is that the third party has a better knowledge of current events than the Republicans. The other two tests are not significant enough to support either alternate hypothesis. It seems that by looking at the histograms of the data, we can see how the other two claims may be true but they are not significant to be counted. So therefore we can’t conclude anything between the Democrats and Republicans or between the Democrats and third parties.
Using our data we can confirm some of our original hypothesis such as that fact that Republicans are not up to date with current events. They had the lowest mean test score and their scores were shown to be significantly low compared to third party scores. We were wrong in thinking that Democrats had the highest knowledge due to the higher mean of the third party. Despite this fact, the test between the two proved not significant so we can’t conclude anything about the two groups.
Overall, the credibility of our data has taken many hits from convenience sampling and non-response. This caused our data to be mostly non-significant. We can look to the mean values to compare but this is not the correct way to show comparisons. Possibly with more resources and more time, the idea for this observational study could be carried further.
Appendices
Appendix One: Raw Data
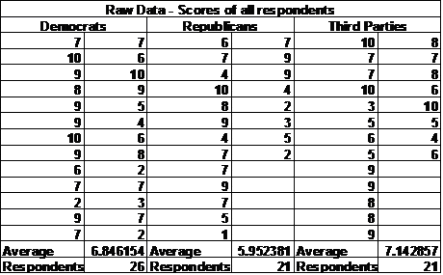
Appendix Two: Bibliography
“Bush supporters misread many of his foreign policy positions” 29 Sept. 2004. Program on
International Policy Attitudes. 2 Jan. 2005.
http://www.pipa.org/OnlineReports/Pres_Election_04/html/new_9_29_04.html
Sullum, Jacob. Knowledge Problems. 15 Oct. 2004. reasononline. 12 Jan. 2005.
http://www.reason.com/sullum/101504.shtml
Lobe, Jim. One World United States. 22 Oct. 2004. OneWorldUS. 15 Jan. 2005.
http://us.oneworld.net/article/view/96543/1/
Wikipedia The Free Online Dictionary, Wikipedia.com, 1/16/05.
Appendix Three: Data Gathering Tool
Current Events Survey
Please write your political affiliation below (i.e, Democrat, Republican, Independent, etc.) :
1. Of what political party is the current president?
a. Democrat
b. Republican
c. Independent
d. Other:
2. What is the current approximate national debt?
a. $14.3 Billion
b. $1.9 Trillion
c. $7.5 Trillion
d. $12.3 Trillion
3. Look at the picture below. Out of the countries below, put an X in Iraq.
4. Which country is not a permanent member of the United Nations Security Council?
a. USA
b. Russia
c. Britain
d. Germany
5. How many political parties does the Constitution call for?
a. No mentioned political parties.
b. Two mentioned political parties.
c. Four mentioned political parties.
d. Six mentioned political parties.
6. In which country did the majority of the 9/11 terrorists originate?
a. Iraq
b. Afghanistan
c. Saudi Arabia
d. Iran
7. Who is the current Prime Minister of the United Kingdom?
a. Winston Churchill
b. Michael Faraday
c. Tony Blair
d. William Blake
8. What is the current problem going on in Ukraine?
a. Elections
b. Nuclear Standoff
c. Terrorists
d. Civil War
9. What position did Donald Rumsfeld hold in President Bush’s Cabinet from 2001-2004?
a. Attorney General
b. Secretary of Defense
c. Secretary of State
d. Head of Homeland Security Department
10. Who was Yasser Arafat?
a. Terrorist involved with world trade center bombings
b. Israel’s Prime Minister
c. Secretary-General of the United Nations
d. Head of the Palestinian Liberation Organization